ДАГЕСТАНСКИЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

ПЕДАГОГИЧЕСКИХ КАДРОВ

КАФЕДРА ФИЗИКО- МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ И ИКТ

Проект

на тему:

« Построение и п реобразования

графиков функций

в школьном курсе математики »

Рабаданова П.А.

учитель математики

МБОУ « Кочубейская СОШ»

Тарумовский район

2015 г.

1. Введение……………………………………………………………….….3

2. Глава I . Обзор литературы по теме проекта………………………….….5

3. Глава II . Эмпирическая часть:

3.1. Основные методы преобразования графиков функции……….….7

3.2. Построение графиков четной и нечетной функций…………….. 10

3.3. Построение графика обратной функции………………………... 11

3.4. Деформация (сжатие и растяжение) графиков ………………….12

3.5.Комбинация переноса, отражения и деформации………………......13

4.Задания для самостоятельного решения………………………..…...14

5.Заключение………………………………………………………………15

6. Выводы…………………………………………………………..………17

ВВЕДЕНИЕ

Преобразование графиков функции является одним из фундаментальных математических понятий, непосредственно связанные с практической деятельностью. В графиках отражены изменчивость и динамичность реального мира, взаимные отношения реальных объектов и явлений.

Функциональная линия является базовой тематикой, рассматриваемая в Основном и Едином государственных экзаменах. Так же многие математические понятия рассматриваются графическими методами. Например, к вадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами. Отсюда следует, что обучение учащихся построению и преобразованию графиков функции является одной из главных задач обучению математике в школе.

Исследование функции дает возможность найти об ласть определения и область значения функции, обла сти убывания или возрастания, асимптоты, интервалы знакопостоянства и др. Однако для построения графи ков многих функций можно использовать ряд методов, облегча ющие построение. Поэтому учащиеся должны иметь компетенции построения графиков по методическим схемам.

Выше сказанное определяет актуальность темы исследования.

Объектом исследования является изучение преобразование графиков функциональной линии в школьной математике.

Предмет исследования – процесс построение и преобразование графиков функции в общеобразовательной школе.

Цель исследования: образовательная - заключается в выявлении методической схемы построения и преобразования графиков функции; развивающая - развитие абстрактного, алгоритмического, логического мышления, пространственного воображения; воспитательная – воспитание графической культуры школьников, формирование навыков умственного труда.

Цели обусловили решение следующих задач:

1. Проанализировать учебно-методическую по исследуемой проблеме.

2. Выявить методические схемы преобразования графиков функции в школьном курсе математики.

3. Отобрать наиболее эффективные методы и средства построение и преобразование графиков функции в общеобразовательной школе , способствующие: осмысленному усвоению учебного материала; повышению познавательной активности учащихся; развитию их творческих способностей.

ГИПОТЕЗА исследования: формирование графических навыков в процессе изучения функций и воспитание графической культуры учащихся будет эффективным, если учащиеся владеют методической схемой построения и преобразования графиков функции в школьном курсе математики.

ГЛАВА I . ОБЗОР ЛИТЕРАТУРЫ ПО ТЕМЕ ПРОЕКТА.

При подготовке к проекту мы изучили следующую литературу:

Сивашинский, И. Х. Теоремы и задачи по алгебре, элементарным функциям - М., 2002. - 115 с.

Гельфанд, И. М., Глаголева, Е. Г., Шноль, Э. Э. Функции и графики (основные приемы) - М., 1985. - 120 с

В.З.Зайцев, В.В. Рыжков, М.И. Сканави. Элементарная математика- М., 2010(переиздание). - 590 с.

Кузьмин, М. К. Построение графика функции - Ж. Математика в школе. - 2003. - №5. - С. 61-62.

Шилов Г.Е. Как строить графики? - М., 1982.

Исаак Танатар. Геометрические преобразования графиков функций - МЦНМО, 2012

В отмечено, что умение с помощью графика «прочитать» поведение функции на некотором множестве находит применение не только в курсе математики, но и в любой практической деятельности человека, в которой ему приходится иметь дело с теми или иными графическими изображениями зависимостей. Поэтому учащиеся должны уметь по графику функции определить некоторые ее свойства.

В строго изложен теоретический материал преобразования графиков. Сопровождается методика иллюстрацией рисунками, различной сложности примерами и их решениями, что дает возможность углублено расширить знания и построении графиков сложных функций.

Представляет электронный учебный курс, объем и содержание которого соответствуют требованиям к курсу математики старших классов средней школы. Теоретический материал подкреплен графическими анимационными иллюстрациями, которые дают наглядные представления об изучаемой теме. Курс включает три модуля: модуль изучения теоретического материала, модуль самопроверки и модуль контроля знаний.

Из , , использованы для эмпирической части проекта методические схемы построения графиков, примеры для самостоятельной работы.

Выводы к 1 главе

Изучение учебно-методической литературы позволило:

1. Выявить методическую схему изучения, построения и преобразования графиков функции в школьном курсе математики.

2. Отобрать наиболее эффективные методы и средства построение и преобразование графиков функции в школьной математике, способствующие:

осмысленному усвоению учебного материала;

повышению познавательной активности учащихся;

развитию их творческих способностей.

3. показать, что функциональная линия оказывает существенное влияние при изучении различных понятий в математике.

Глава 2. ЭМПИРИЧЕСКАЯ ЧАСТЬ

В этой главе мы рассмотрим основные методы преобразования графиков функций, дадим методические схемы построения различных комбинаций графиков для различных функций.

2.1. ОСНОВНЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИИ

Перенос вдоль оси ординат

f ( x ) f ( x )+ b .

Для построения графика функции y = f ( x ) + b следу ет:

1. построить график функции y = f ( x )

2. перенести ось абсцисс на | b | единиц вверх при b >0 или на | b | еди ниц вниз при b < 0. Полученный в новой системе коор динат график является графиком функции y = f ( x ) + b .

2. Перенос вдоль оси абсцисс

f ( x ) f ( x + a ) .

y = f ( x + a ) следу ет:

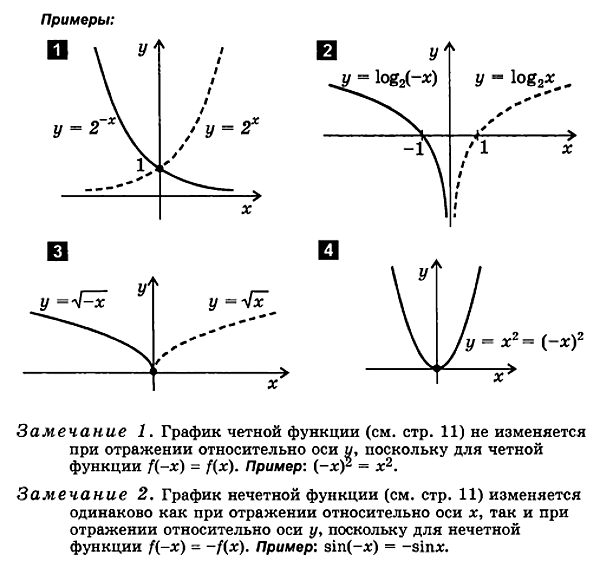
3. Построение графика функции вида y = f (- x )

f (x ) f (- x ).

Для построения графика функции y = f ( - х) следует:

построить график функции y = f ( x )

отразить его отно сительно оси ординат

полученный график является графиком функции y = f ( - х).

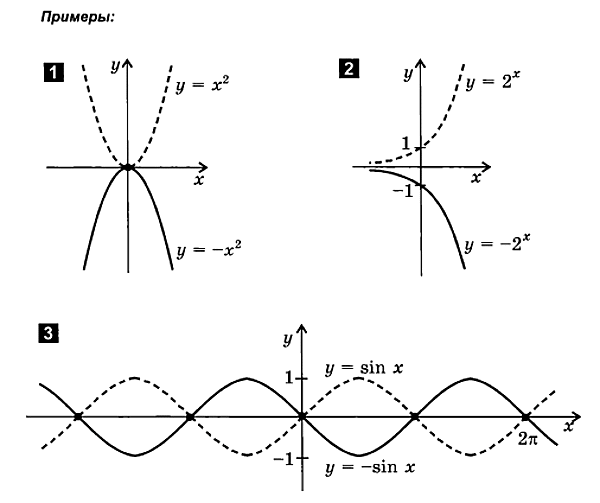
4. Построение графика функции вида у = - f ( x )

f ( x ) - f ( x )

- f ( x ) следует:

построить график функции y = f ( x )

отразить его относительно оси абсцисс

2.2. Построение графиков четной и нечетной функций

При построении графиков четной и нечетной функции удобно пользоваться следующими свойствами:

1.График четной функции симмет ричен относительно оси ординат.

2. График нечетной функции симметричен относительно начала координат.

Для построения графиков четной и нечетной функции достаточно построить только правую ветвь графика для положительных значений аргумента. Левая ветвь достраивается симметрично относительно начала координат для нечетной функции и относительно оси ординат для четной функции.

Для построения графика четной функции y = f ( x ) сле дует:

построить ветвь графика этой функции только в об ласти положительных значений аргумента х≥О.

О тразить этот ветвь относительно оси ординат

Для построения графика нечетной функции y = f ( x ) следует:

строить ветвь графика этой функции только в области положительных значений аргумента (х≥0).

О тразить этот ветвь относительно начало координат в область отрицательных значений х.

2.3. Построение графика обратной функции

Как уже отмечалось, прямая и обратная функции вы ражают одну и ту же зависимость между переменными х и у, с тем только отличием, что в обратной функции эти переменные поменялись ролями, что равносильно изме нению обозначений осей координат. Поэтому график обратной функции симметричен графику прямой функции относительно биссектрисы I и III координатных углов, т. е. относительно прямой у = х. Таким образом, получаем следующее правило.

Для построения графика функции у = (х), обратной по отношению к функции y = f ( x ), следует построить график y = f ( x ) и отразить его относительно прямой у = х.

2.4. Деформация (сжатие и растяжение) графиков

1. Сжатие (растяжение) графика вдоль оси ординат

f ( x ) A ∙ f ( x ).

Для построения графика функции y = A ∙ f ( x ) следует:

8. Сжатие (растяжение) графика вдоль оси абсцисс

f ( x )

Для построения графика функции у = f ( x ) следует:

2.5. Комбинация переноса, отражения и деформации

Очень часто при построении графиков функций при меняют комбинацию приемов .

Последовательное применение ряда таких приемов поз воляет существенно упростить построение графика ис ходной функции и нередко свести его в конце концов к построению одной из простейших элементарных функ ций. Рассмотрим, как с учетом изложенного следует строить графики функций.

Отметим, что поря док упрощения целесообразно проводить в следующей последователь ности.

Использование четности или нечетности функции.

Перенос осей.

Отражение и деформация.

Построение же графика выполняется в обратной последовательности.

Пример. Построить график функции

Построение проведем по следующим шагам:

1. построим график натурального логарифма :

2. сожмём к оси OY в 2 раза: ;
3. отобразим симметрично относительно оси OY : ;
4. сдвинем вдоль оси OX на (!!!) вправо: :

5. отобразим симметрично относительно оси OX : ;
6. сдвинем вдоль оси OY на 3 единицы вверх: :

ПРИМЕРЫ ПОСТРОЕНИЯ и ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИИ

Пример 1. Построить график функции .

Сначала изобразим график синуса, его период равен :

график функции получается путём сжатия графика к оси ординат в два раза. log .

Построить график функции у = 2 cos х.

Построить график функции y = sin x .

ЗАКЛЮЧЕНИЕ

Во время работы над проектной работой были проанализирована различная учебно-методическая литература по данной проблеме. Результаты исследования позволили выявить наиболее характерные положительные стороны изучения , построения и преобразования графиков функции в школьном курсе математики

Основной целью проекта является формирование у учащихся умений и навыков в чтении и выполнении чертежей, в формировании у них рациональных приемов самостоятельной деятельности.

Необходимость усовершенствования графического образования в целом диктуется не только современными требованиями производства, но и ролью графики в развитии технического мышления и познавательных способностей учащихся. Способность человека к переработке графической информации является одним из показателей его умственного развития. Поэтому графическая подготовка должна стать неотъемлемым элементом общеобразовательной подготовки.

Выводы

Таким образом, разработанный проект « Построение и преобразование графиков функции», посвященный одному из центральных понятий математики - функциональной зависимости, ориентирован на систематизацию и расширение знаний учащихся. Изучение конкретных способов преобразования графиков функций проводится аналитико-графическим путем по строгим методическим схемам. Собранный материал можно использовать на уроках и для самоподготовки учащихся. Для проведения занятий могут использоваться разнообразные формы и методы организации и обучения.

Показательная функция - это обобщение произведения n чисел, равных a :
y(n) = a n = a·a·a···a ,
на множество действительных чисел x :
y(x) = a x .
Здесь a - фиксированное действительное число, которое называют основанием показательной функции .
Показательную функцию с основанием a также называют экспонентой по основанию a .

Обобщение выполняется следующим образом.
При натуральном x = 1, 2, 3,... , показательная функция является произведением x множителей:
.
При этом она обладает свойствами (1.5-8) (), которые следуют из правил умножения чисел. При нулевом и отрицательных значениях целых чисел , показательную функцию определяют по формулам (1.9-10). При дробных значениях x = m/n рациональных чисел, , ее определяют по формуле(1.11). Для действительных , показательную функцию определяют как предел последовательности:
,
где - произвольная последовательность рациональных чисел, сходящаяся к x : .
При таком определении, показательная функция определена для всех , и удовлетворяет свойствам (1.5-8), как и для натуральных x .

Строгая математическая формулировка определения показательной функции и доказательство ее свойств приводится на странице «Определение и доказательство свойств показательной функции ».

Свойства показательной функции

Показательная функция y = a x , имеет следующие свойства на множестве действительных чисел () :
(1.1) определена и непрерывна, при , для всех ;
(1.2) при a ≠ 1 имеет множество значений ;
(1.3) строго возрастает при , строго убывает при ,
является постоянной при ;
(1.4) при ;
при ;
(1.5) ;
(1.6) ;
(1.7) ;
(1.8) ;
(1.9) ;
(1.10) ;
(1.11) , .

Другие полезные формулы.
.
Формула преобразования к показательной функции с другим основанием степени:

При b = e , получаем выражение показательной функции через экспоненту:

Частные значения

, , , , .

На рисунке представлены графики показательной функции
y(x) = a x
для четырех значений основания степени : a = 2 , a = 8 , a = 1/2 и a = 1/8 . Видно, что при a > 1 показательная функция монотонно возрастает. Чем больше основание степени a , тем более сильный рост. При 0 < a < 1 показательная функция монотонно убывает. Чем меньше показатель степени a , тем более сильное убывание.

Возрастание, убывание

Показательная функция, при является строго монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.

	y = a x , a > 1	y = a x , 0 < a < 1
Область определения	- ∞ < x < + ∞	- ∞ < x < + ∞
Область значений	0 < y < + ∞	0 < y < + ∞
Монотонность	монотонно возрастает	монотонно убывает
Нули, y = 0	нет	нет
Точки пересечения с осью ординат, x = 0	y = 1	y = 1
	+ ∞	0
	0	+ ∞

Обратная функция

Обратной для показательной функции с основанием степени a является логарифм по основанию a .

Если , то
.
Если , то
.

Дифференцирование показательной функции

Для дифференцирования показательной функции, ее основание нужно привести к числу e , применить таблицу производных и правило дифференцирования сложной функции.

Для этого нужно использовать свойство логарифмов
и формулу из таблицы производных :
.

Пусть задана показательная функция:
.
Приводим ее к основанию e :

Применим правило дифференцирования сложной функции . Для этого вводим переменную

Тогда

Из таблице производных имеем (заменим переменную x на z ):
.
Поскольку - это постоянная, то производная z по x равна
.
По правилу дифференцирования сложной функции:
.

Производная показательной функции

.
Производная n-го порядка:
.
Вывод формул > > >

Пример дифференцирования показательной функции

Найти производную функции
y = 3 5 x

Решение

Выразим основание показательной функции через число e .
3 = e ln 3
Тогда
.
Вводим переменную
.
Тогда

Из таблицы производных находим:
.
Поскольку 5ln 3 - это постоянная, то производная z по x равна:
.
По правилу дифференцирования сложной функции имеем:
.

Ответ

Интеграл

Выражения через комплексные числа

Рассмотрим функцию комплексного числа z :
f(z) = a z
где z = x + iy ; i 2 = - 1 .
Выразим комплексную постоянную a через модуль r и аргумент φ :
a = r e i φ
Тогда


.
Аргумент φ определен не однозначно. В общем виде
φ = φ 0 + 2 πn ,
где n - целое. Поэтому функция f(z) также не однозначна. Часто рассматривают ее главное значение
.

Разложение в ряд

.

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Какие из данных функций имеют обратную? Для таких функций найти обратные функции:

4.12. а)	y = x ;					б) y = 6 −3 x ;
г) y =						д) y = 2 x 3 +5 ;
4.13. а)	y = 4 x − 5 ;						y = 9 − 2 x − x 2 ;
	y = sign x ;						y =1 + lg(x + 2) ;

	y = 2 x 2 +1 ;
			x − 2
						при x < 0
в) y =		−x
						при x ≥ 0

Выяснить, какие из данных функций монотонны, какие – строго монотонны, а какие – ограничены:

4.14. а)

f (x) = c, c R ;

б) f (x ) = cos 2 x ;

в) f (x ) = arctg x ;

г) f (x ) = e 2 x ;

д) f (x ) = −x 2 + 2 x ;

е) f (x ) =

2x + 5

y = ctg7 x .

4.15. а)

f (x ) = 3− x

б) f (x ) =

f (x) =

x + 3

x + 6

x < 0,

3x + 5

г) f (x ) = 3 x 3 − x ;

− 10 при

f (x) =

д) f (x ) =

x 2 при

x ≥ 0;

x + 1

f (x ) = tg(sin x ).

4.2. Элементарные функции. Преобразование графиков функций

Напомним, что графиком функции f (x ) в декартовой прямоугольной системе координат Oxy называется множество всех точек плоскости с координатами (x , f (x )) .

Часто график функции y = f (x ) можно построить с помощью преобразований (сдвиг, растяжение) графика некоторой уже известной функции.

В частности, из графика функции y = f (x ) получается график функции:

1) y = f (x ) + a – сдвигом вдоль оси Oy на a единиц (вверх, если a > 0 , и вниз, если a < 0 ;

2) y = f (x −b ) – сдвигом вдоль оси Ox на b единиц (вправо, если b > 0 ,

и влево, если b < 0 ;

3) y = kf (x ) – растяжением вдоль оси Oy в k раз;

4) y = f (mx ) – сжатием по оси Ox в m раз;

5) y = − f (x ) – симметричным отражением относительно оси Ox ;

6) y = f (−x ) – симметричным отражением относительно оси Oy ;

7) y = f (x ) , следующим образом: часть графика, расположенная не

ниже оси Ox , остается без изменений, а «нижняя» часть графика симметрично отражается относительно оси Ox ;

8) y = f (x ) , следующим образом: правая часть графика (при x ≥ 0 )

остается без изменений, а вместо «левой» строится симметричное отражение «правой» относительно оси Oy .

Основными элементарными функциями называются:

1) постоянная функция y = c ;

2) степенная функция y = x α , α R ;

3) показательная функция y = a x , a ≠ 0, a ≠1 ;

4) логарифмическая функция y = log a x , a > 0, a ≠ 1 ;

5) тригонометрические функции y = sin x , y = cos x , y = tg x ,

y = ctg x , y = sec x (где sec x = cos 1 x ), y = cosec x (где cosec x = sin 1 x );

6) обратные тригонометрические функции y = arcsin x , y = arccos x , y = arctg x , y = arcctg x .

Элементарными функциями называются функции, полученные из основных элементарных функций с помощью конечного числа арифметических операций (+, − , ÷) и композиций (т.е. образования сложных функций f g ).

Пример 4.6. Построить график функции

1) y = x 2 + 6 x + 7 ; 2) y = −2sin 4 x .

Решение: 1) путем выделения полного квадрата функция преобразуется к виду y = (x +3) 2 − 2 , поэтому график данной функции можно получить из графика функции y = x 2 . Достаточно сначала сместить параболу y = x 2 на три единицы влево (получим график функции y = (x +3) 2 ), а затем на две единицы вниз (рис. 4.1);

	стандартную	синусоиду						y = sin x	в четыре раза по оси		Ox ,
получим график функции y = sin 4 x (рис. 4.2).
										y= sin4x
										y=sin x

Растянув полученный график в два раза вдоль оси Oy , получим график функции y = 2sin 4 x (рис. 4.3). Осталось отразить последний график относительно оси Ox . Результатом будет искомый график(см. рис. 4.3).

						y= 2sin4x

y=– 2sin4 x

Задачи для самостоятельного решения

Построить графики следующих функции, исходя из графиков основных элементарных функций:

4.16. а) y = x 2 −6 x +11 ;

4.17. а) y = −2sin(x −π ) ;

4.18. а) y = − 4 x −1 ;

4.19. а) y = log 2 (−x ) ;

4.20. a) y = x +5 ;

4.21. а) y = tg x ;

4.22. а) y = sign x ;

4.23. а) y = x x + + 4 2 ;

y = 3 − 2 x − x 2 .

y = 2cos 2 x .

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Введение

Преобразование графиков функции является одним из основных математических понятий, непосредственно связанные с практической деятельностью. Преобразование графиков функций впервые встречается в алгебре 9 класса при изучении темы «Квадратичная функция». Квадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами. Так же многие математические понятия рассматриваются графическими методами, например в 10 - 11 классах исследование функции дает возможность найти область определения и область значения функции, области убывания или возрастания, асимптоты, интервалы знакопостоянства и др. Так же этот немаловажный вопрос выносится на ГИА. Отсюда следует, построение, и преобразование графиков функции является одной из главных задач обучения математике в школе.

Однако для построения графиков многих функций можно использовать ряд методов, облегчающих построение. Выше сказанное определяет актуальность темы исследования.

Объектом исследования является изучение преобразование графиков в школьной математике.

Предмет исследования - процесс построение и преобразование графиков функции в общеобразовательной школе.

Проблемный вопрос : можно ли построить график не знакомой функции, имея навык преобразования графиков элементарных функций?

Цель: построение графиков функции в незнакомой ситуации.

Задачи:

1. Проанализировать учебный материал по исследуемой проблеме. 2. Выявить схемы преобразования графиков функции в школьном курсе математики. 3. Отобрать наиболее эффективные методы и средства построение и преобразование графиков функции. 4.Уметь применять данную теории в решении задач.

Необходимые начальные знания, умения, навыки:

Определять значение функции по значению аргумента при различных способах задания функции;

Строить графики изученных функций;

Описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;

Описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.

Основная часть

Теоретическая часть

В качестве исходного графика функции y = f(x) выберу квадратичную функциюy = x 2 . Рассмотрю случаи преобразования данного графика, связанные с изменениями формулы, задающей эту функцию и сделаю выводы для любой функции.

1. Функция y = f(x) + a

В новой формуле значения функции (ординаты точек графика) изменяются на число a, по сравнению со «старым» значением функции. Это приводит к параллельному переносу графика функции вдоль оси OY:

вверх, если a > 0; вниз, если a < 0.

ВЫВОД

Таким образом график функции y=f(x)+a, получается из графика функции y=f(x) с помощью параллельного переноса вдоль оси ординат на a единиц вверх, если a > 0, и на a единиц вниз, если a < 0.

2. Функция y = f(x-a),

В новой формуле значения аргумента (абсциссы точек графика) изменяются на число a, по сравнению со «старым» значением аргумента. Это приводит к параллельному переносу графика функции вдоль оси OX: вправо, если a < 0, влево, если a >0.

ВЫВОД

Значит график функции y= f(x - a), получается из графика функции y=f(x) с помощью параллельного переноса вдоль оси абсцисс на a единиц влево, если a > 0, и на a единиц вправо, если a < 0.

3. Функция y = k f(x), где k > 0 и k ≠ 1

В новой формуле значения функции (ординаты точек графика) изменяются в k раз, по сравнению со «старым» значением функции. Это приводит к: 1) «растяжению» от точки (0; 0) вдоль оси ОY в k раз, если k > 1, 2) «сжатию» к точке (0; 0) вдоль оси OY в раз, если 0 < k < 1.

ВЫВОД

Следовательно: чтобы построить график функции y = kf(x), где k > 0 и k ≠ 1 нужно ординаты точек заданного графика функции y = f(x) умножить на k. Такое преобразование называется растяжением от точки (0; 0) вдоль оси ОY в k раз, если k > 1; сжатием к точке (0; 0) вдоль оси OY в раз, если 0 < k < 1.

4. Функция y = f(kx), где k > 0 и k ≠ 1

В новой формуле значения аргумента (абсциссы точек графика) изменяются в k раз, по сравнению со «старым» значением аргумента. Это приводит к: 1) «растяжению» от точки (0; 0) вдоль оси ОX в 1/k раз, если 0 < k < 1; 2) «сжатию» к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

ВЫВОД

И так: чтобы построить график функции y = f(kx), где k > 0 и k ≠ 1 нужно абсциссы точек заданного графика функции y=f(x) умножить на k. Такое преобразование называется растяжением от точки (0; 0) вдоль оси ОX в 1/k раз, если 0 < k < 1, сжатием к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

5. Функция y = - f (x).

В данной формуле значения функции (ординаты точек графика) изменяются на противоположные. Это изменение приводит к симметричному отображению исходного графика функции относительно оси Ох.

ВЫВОД

Для построения графика функции y = - f (x) необходимо график функции y= f(x)

симметрично отразить относительно оси OX. Такое преобразование называется преобразованием симметрии относительно оси OX .

6. Функция y = f (-x).

В данной формуле значения аргумента (абсциссы точек графика) изменяются на противоположные. Это изменение приводит к симметричному отображению исходного графика функции относительно оси ОY.

Пример для функции у = - х² это преобразование не заметно, т. к. данная функция чётная и график после преобразования не меняется. Это преобразование видно, когда функция нечётная и когда ни чётная и ни нечётная.

7. Функция y = |f(x)|.

В новой формуле значения функции (ординаты точек графика) находятся под знаком модуля. Это приводит к исчезновению частей графика исходной функции с отрицательными ординатами (т.е. находящихся в нижней полуплоскости относительно оси Ох) и симметричному отображению этих частей относительно оси Ох.

8. Функция y= f (|x|).

В новой формуле значения аргумента (абсциссы точек графика) находятся под знаком модуля. Это приводит к исчезновению частей графика исходной функции с отрицательными абсциссами (т.е. находящихся в левой полуплоскости относительно оси ОY) и замещению их частями исходного графика, симметричными относительно оси ОY.

Практическая часть

Рассмотрим несколько примеров применения вышеизложенной теории.

ПРИМЕР 1.

Решение. Преобразуем данную формулу:

1) Построим график функции

ПРИМЕР 2.

Построить график функции, заданной формулой

Решение. Преобразуем данную формулу, выделив в данном квадратном трехчлене квадрат двучлена:

1) Построим график функции

2) Выполним параллельный перенос построенного графика на вектор

ПРИМЕР 3.

ЗАДАНИЕ ИЗ ЕГЭПостроение графика кусочной функции

График функции График функции y=|2(x-3)2-2|; 1

В зависимости от условий протекания физических процессов одни величины принимают постоянные значения и называются константами, другие - изменяются в определенных условиях и называются переменными.

Внимательное изучение окружающей среды показывает, что физические величины зависимы друг от друга, т. е. изменение одних величин влечет за собой изменение других.

Математический анализ занимается изучением количественных соотношений взаимно -изменяющихся величин, отвлекаясь от конкретного физического смысла. Одним из основных понятий математического анализа есть понятие функции.

Рассмотрим элементы множества и элементы множества
(рис. 3.1).

Если устанавливается некоторое соответствие между элементами множеств
и в виде правила , то тем самым отмечают, что определяется функция
.

Определение 3.1. Соответствие, которое связывает с каждым элементомне пустого множества
некоторый, вполне определенный, элементне пустого множества ,называется функцией или отображением
в .

Символически отображение
в записывается следующим образом:

.

При этом множество
называется областью определения функции и обозначается
.

В свою очередь, множество называется областью значений функции и обозначается
.

Кроме того, необходимо отметить, что элементы множества
называют независимыми переменными, элементы множества называют зависимыми переменными.

Способы задания функции

Функция может задаваться следующими основными способами: табличным, графическим, аналитическим.

Если на основании экспериментальных данных составляют таблицы, в которых содержатся значения функции и соответствующие им значения аргумента, то такой способ задания функции называют табличным.

В то же время, если некоторые исследования результата эксперимента выводят на регистратор (осциллограф, самописец и т. д.), то отмечают, что функция задается графически.

Наиболее распространенным есть аналитический способ задания функции, т.е. способ, при котором с помощью формулы связывают независимую и зависимую переменные. При этом существенную роль играет область определения функции:

разные, хотя они и задаются одинаковыми аналитическими соотношениями.

Если задают только формулу функции
, то считают, что область определения этой функции совпадает с множеством тех значений переменной, для которых выражение
имеет смысл. В этой связи особую роль играет проблема нахождения области определения функции.

Задача 3.1. Найти область определения функции

Решение

Первое слагаемое принимает действительные значения при
,а второе при. Таким образом, для нахождения области определения заданной функции необходимо решить систему неравенств:

В результате решения такой системы получают . Следовательно, область определения функции есть отрезок
.

Простейшие преобразования графиков функций

Построение графиков функций можно существенно упростить, если пользоваться известными графиками основных элементарных функций. Основными элементарными функциями называются следующие функции:

1)степенная функция
где
;

2)показательная функция
где
и
;

3)логарифмическая функция
, где -любое положительное число, отличное от единицы:
и
;

4)тригонометрические функции




;
.

5)обратные тригонометрические функции
;
;
;
.

Элементарными функциями называются функции, получающиеся из основных элементарных функций с помощью четырех арифметических действий и суперпозиций, примененных конечное число раз.

Простые геометрические преобразования также позволяют упростить процесс построения графика функций. Эти преобразования основываются на следующих утверждениях:

График функции y=f(x+a) есть графикy=f(x), сдвинутый (при a >0 влево, при a < 0 вправо) на |a| единиц параллельно осиOx.

График функции y=f(x) +bесть графикy=f(x), сдвинутый (приb>0 вверх, приb< 0 вниз) на |b| единиц параллельно осиOy.

График функции y = mf(x) (m0) есть график y = f(x), растянутый (приm>1) вmраз или сжатый (при 0

График функции y = f(kx) есть график y = f(x), сжатый (при k >1) в k раз или растянутый (при 0< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx) есть зеркальное отображение графика y = f(–kx) от оси Oy.